
Por representación entendemos las distintas formas de modelar un objeto. Esto es, las distintas estructuras de datos que nos permiten guardar las características de un objeto tridimensional en la memoria de la computadora.
Las mediciones realizadas por los equipos TAC son "puntuales". O sea, obtienen el valor de la densidad del tejido en el punto de aplicación. Sin embargo, debido a condicionamientos técnicos obtenemos una mayor densidad de mediciones sobre un "plano" (o corte) determinado que cantidad de cortes sobre el objeto de estudio.
Es muy conveniente trabajar con voxels cúbicos. Esto permite una mejor triangulación de los datos, mayor suavidad en las superficies, como así también una selección más inteligente de los voxels de interés.
El conjunto de datos con los que se trabajará tiene una resolución en el plano X-Y de la imagen mucho mayor que la resolución en Z, que esta en función de la cantidad de cortes del estudio (o número de slices)..

Cada valor dentro del conjunto de datos representa, en el caso de TAC, la densidad de tejido en ese punto. Observando la (Figura 4-1) se aprecia que el resultado del Sub-Sampling supone la misma densidad a lo largo de todo el espacio entre un corte y el siguiente, del cual se carece de información.
Teniendo en cuenta que la resolución en el plano X-Y varía normalmente entre los 0,4 y 1,5 milimetros y la separación entre cortes (resolución en Z), va de 2mm, en el mejor de los casos, a 10 mm, se tiene la siguiente relación:

Es decir, el error del volumen estimado con el volumen cúbico deseado va, desde 33.33% en el mejor de los casos (cuando la resolución en pantalla es mínima y la cantidad de cortes máxima), a 2400 % en el peor de los casos
La cantidad de cortes a generar mediante interpolación se obtiene dividiendo el espacio entre cortes por la resolución en XY, el plano transversal.

Se tiene entonces la situación mostrada en la (Figura 4-2). Es necesario determinar la intensidad del voxel intermedio.
El método clásico es interpolar linealmente las intensidades de los voxel extremos [RAY90]. Esta interpolación es función de la posición y es adecuada para lograr aproximaciones simples. Más adelante se detallan los problemas relacionados con esta aproximación.
Este algoritmo de interpolación con algunos valores de ejemplo, resultaría en algo similar a lo mostrado en la (Figura 4-3).
La función de interpolación viene dada por:
Donde A y B son las intensidades medidas de los voxels en los slices extremos y d es la distancia (normalizada) entre el voxel con intensidad A y el voxel a interpolar.
Este método para obtener más cortes, si bien es adecuado para una primera aproximación tiene la desventaja de no mejorar significativamente la suavidad de las superficies una vez reconocidos los objetos.

En los bordes de los objetos, se presentan abruptos cambios en la intensidad de los voxels de distintos cortes. Este abrupto cambio de intensidad, acoplado con el método de reconocimiento de formas mas utilizado, el del umbral, tiende a producir superficies con bordes abruptos o discontinuidades.
A modo de ejemplo, supóngase tener dos cortes muestreados con los siguientes valores de intensidad:

El borde mostrado divide las regiones de objeto y no-objeto, habiendose utilizado 136 como valor de umbral para la desición.
Se puede observar lo abrupto del cambio de posición del borde (debido a la cantidad de separación de los cortes en relación con la velocidad de cambio de la superficie en esa zona). Mientras que en el corte n, la posición del borde estaría en el tercer voxel, en el corte siguiente la posición cambia al voxel octavo, provocando el clásico escalonamiento.
Sin embargo, interpolando linealmente los cortes mostrados y utilizando 136 nuevamente como valor umbral, se tendría lo siguiente:

Se observa que la interpolación lineal directa de intensidades no ha mejorado en mucho la discontinuidad en el borde. Esto es el resultado de utilizar un método de reconocimiento simple como el de umbral, pero éste es el más usado en aplicaciones de medical imaging, que son útiles para éste trabajo.
Recientemente se han presentado [HER92] trabajos para obtener los cortes interpolados sin sufrir este problema. Estos métodos, basados en el estudio de las discontinuidades luego de reconocer los bordes en cada corte, son muy recientes y, por lo tanto, no fueron evaluados por nosotros como para presentar un juicio de valor de los mismos.
Un aspecto importante que hay que tener en cuenta en el proceso de obtención del volúmen cúbico de datos es el del almacenamiento. La generación de slices adicionales a los del estudio original significa un aumento muy importante en la cantidad de datos del modelo. Teniendo en cuenta las resoluciones en los tres planos antes mencionadas, se pueden crear entre 2 y 25 cortes adicionales entre cada par de cortes muestreados. Si cada corte tiene aproximadamente 512 x 512 pixels (512 x 512 bytes, suponiendo 1 byte por pixel) de resolución en X,Y, y un estudio simple se compone de 15 a 20 placas, se tendrían los siguientes requerimientos de almacenamiento:
N = Número de cortes muestreado
ResX = Resolución (cantidad de pixels) en X
ResY = Resolución (cantidad de pixels) en Y
CInterp = Cantidad de Cortes artificiales a generar entre cada par de cortes
Los requerimientos mínimos y máximos para almacenar 15 y 20 placas entre 2 y 25 cortes adicionales serían los siguientes:
(mejor caso) A = 512 * 512 * (15 + (15 - 1) * 2) = 11272192 Bytes (11MB)
(peor caso) A = 512 * 512 * (20 + (20 - 1) * 25) = 129761280 Bytes (124MB)
Si bien estos datos pueden ser compactados de alguna manera, en algún momento deben ser procesados. Es por esto que para trabajar con Volume Rendering - que se basa en el procesamiento de cada elemento de volumen-, en oposición a Surface Rendering -que se basa en el procesamiento de entidades matemáticas que representan al volumen-, se necesitan workstations especiales con gran velocidad de proceso. (Los conceptos de Volumen y Surface Rendering son explicados con mayor detalle en el párrafo § 4.3.)
Es importante hacer notar que en todos los cálculos arriba expuestos, se asumió que un voxel equivale a un byte de almacenamiento (8 bits). Si bien esta es un suposición razonable (especialmente en nuestro caso en que la adquisición de datos fue realizada mediante equipos "entorno PC" -que generalmente trabajan con resoluciones de 1 byte por pixel-) no es del todo exacta, ya que la mayoría de los equipos de TAC trabajan con una resolución de 12 bits (1.5 byte) por voxel (pixel).
La utilidad de las distintas técnicas de medical imaging radica en la posibilidad de poder hacer una visualización no-invasiva del órgano de interés. Hasta el momento, no tenemos en nuestro volumen de datos más que una serie de mediciones de la densidad del tejido en el punto de medición.
Si bien, como se verá mas adelante, estos datos permitirían hacer cualquier tipo de cortes (axiales, sagitales, coronales o en cualquier orientación), extendiendo notablemente la posibilidad de los equipos de TAC estándares, el objetivo es obtener, de todo el volúmen de datos, el órgano que estamos interesados en estudiar.
La tarea de reconocer un objeto dentro del volúmen podría resumirse en:

El conjunto C de voxels será el volúmen sobre el cual se trabajará. En C, cada voxel tiene el valor de intensidad medido por el equipo TAC (o generado por interpolación).
El conjunto O de voxels es el resultado deseado. Este conjunto puede ser del mismo tamaño o menor que C. Puede estar implementado (como se hace a menudo) como un escena binaria (binary scene), donde O es del mismo tamaño que C, con la salvedad que todos los voxels pertenecientes al objeto se marcan como "OBJETO" y el resto como "NO OBJETO".
La creación de S, la función de segmentación, no es una tarea simple. Por el contrario, es un área en constante investigación y progreso sobre la cual todavía no se ha podido dar una respuesta definitiva (o aún mas, satisfactoria) [HER83].
En el área de medical imaging, los intentos se pueden resumir en:
Este método emplea una "biblioteca" de imágenes "verdaderas". O sea, se generan, con validación de los especialistas en el área, un serie de imágenes de TAC de distintas partes del cuerpo a distintos niveles, señalándosé en cada una los distintos objetos que la componen (por ejemplo, hueso, piel, etc). Luego de generada esta biblioteca, se parametrizan ciertos aspectos de las imágenes (como ser, tamaño longitudinal del cráneo) para luego poder hacer la comparación con las tomografías de los distintos pacientes.
Esta metodología es el intento más completo y complejo de los tres arriba mencionados. Sin embargo, adolece de ciertas dificultades importantes:
Algunos trabajos han intentado introducir marcadores en el campo de visión para que sean registrados por el equipo TAC, y luego puedan ser utilizados como parámetros "índice" de la biblioteca. Se han logrado resultados importantes restringiendo el espectro de usos posibles (por ejemplo, solamente estudios de cadera).
La segmentación interactiva implica la ayuda de un especialista en las imágenes que están siendo estudiadas. Se van presentando las imágenes de los distintos cortes en forma sucesiva y el especialista (radiólogo, médico, etc) marca con algún dispositivo de entrada las zonas pertenecientes al objeto.
Este método es el que tiene el menor porcentaje de error, ya que utiliza el conocimiento del experto para segmentar las imágenes. A menudo, se usa como base de referencia sobre la cual comparar todas las demás imágenes.
La mayor complicación de este método es la necesidad de disponer de un especialista en diagnóstico por imágenes para cada estudio (y por cada imagen generada por el equipo de TAC). Debido a esto, la segmentación interactiva se utiliza normalmente en la generación de volúmenes de datos "maestros" (por ejemplo, para formar la "biblioteca" mencionada en 4.2.1).
En el caso particular del presente trabajo, se utilizó un cierto nivel de interactividad para solucionar los problemas introducidos por la adquisición de las imágenes mediante scanner. Sin embargo, nuestra "segmentación" se limitó a separar las partes no corpóreas de la imágen (barras de control, letras, etc), dejando la segmentación dentro del cuerpo para el método que se verá a continuación.
La segmentación por threshold (umbral) es la más simple y la más utilizada en la identificación de hueso, que es el órgano de interés abordado en este trabajo. Además, tiene resultados aceptables y requerimientos computacionales modestos.
La idea detrás de este algoritmo es clasificar cada elemento de volúmen según sus propiedades intrínsecas, medidas por el tomógrafo, como OBJETO o NO-OBJETO (parte del órgano o nó). Generalmente se determinan, de forma experimental, valores de umbral adecuados para cada tipo de órgano y/o para cada estudio distinto. Vale la pena hacer notar que, si bién la determinación exacta de los umbrales requiere cierto nivel de interactividad, puede ser realizado muy rápidamente en la misma consola por el operador del equipo TAC.
Una vez determinados los umbrales el algoritmo es simple, y consiste en [FU88]:
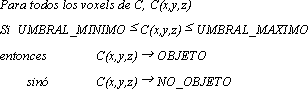
Este algoritmo, aplicado a una imágen de TAC de la parte superior del craneo, nos dá como resultado algo similar a lo mostrado en la (Figura 4-5).
Todos los métodos arriba mencionados generan como resultado una escena binaria, definiendose esta como el conjunto de voxels del volumen de datos, previamente procesados de manera tal que cada voxel tenga uno de dos valores posibles (0 o 1), en función de su pertenencia al objeto de interés.
Una extensión natural de esta representación es la compactación de los datos para disminuir el espacio requerido de almacenamiento.

Suponiendo siempre una resolución por voxel de 8 bits (1 byte), los requerimientos de espacio se reducirían, entonces, a 1/8 del total, empaquetando 8 voxels por byte. Esta disminución del espacio necesario dejaría el rango de espacio necesario (según se vió en 4.1.2) entre 1.4 y 15.5 MB, lo cual es bastante más aceptable. Es importante entender que, a diferencia de otros algoritmos de compactación, esta reducción permite identificar biunívocamente cada voxel del conjunto a partir de su posición en el espacio (o viceversa, determinar la posición en el espacio de un voxel dado a partir de las resoluciones en los tres planos y su posición dentro del archivo). Los métodos de compactación de datos estándares (LZW, RLL, etc) obtendrían porcentajes de ahorro de espacio mucho mayores, pero tienen el gran inconveniente que para acceder a cualquier voxel deben descompactar todo el archivo (o al menos una parte del mismo).
En la escena binaria tenemos toda la información volumétrica que necesitamos para estudiar el objeto de interés.
Dentro del area de Visualización Cientifica (Scientific Visualization) existen dos grandes ramas de representación de objetos tridimensionales:
La visualización por volume rendering se basa en la escena binaria (o inclusive, en los datos originales sin hacer la segmentación, o haciéndola en el momento del display) [FRI85] y es una idea conceptualmente muy atrayente. No se intenta describir al objeto de ninguna manera, simplemente se lo divide en elementos cúbicos muy pequeños (como se vió en 4.1), pudiendose direccionar (esto es, clasificar, esconder, modificar) cada uno de estos. Para lograr la graficación tridimensional de algún objeto mediante este método simplemente se grafican, en el orden adecuado, todos los voxels que lo componen.
El volume rendering es una disciplina con mucho futuro, ya que las capacidades computacionales aumentan a un ritmo impresionante. Como herramienta para la medición, se la considera más exacta que los métodos mas "inteligentes" (que se verán a continuación), ya que describe todos y cada uno de los elementos que componen a un objeto [MIH91] [NIE91] [FOL90].
Los métodos de Surface Rendering describen el objeto mediante aproximaciones matemáticas a las superficies que lo componen. En estos métodos basados en superficies no se distinguen los cambios de intensidad (o densidad) dentro del mismo objeto (ya que se basan en la escena binaria, y esta no preserva el rango de intesidades provista por el equipo TAC),
Existen distintas maneras de representación de superficies en el espacio [BAR82] [FOL90], pero todas se basan en la "figura" (o silueta) del objeto. Las ventajas de estos métodos radican principalmente en la disminución del volumen de datos necesario para describir el objeto, la manejabilidad y maleabilidad de estas estructuras matemáticas y la posibilidad de implementación en equipos de menor porte que los necesarios para los métodos basados en volume rendering.
Existen también estructuras de datos "híbridas", con componentes de ambas metodologías. Una muy utilizada [FRI885] [RAY90] [HER88] es la de generar el volúmen completo de voxels y mantenerlos en "memoria", pero para el display se aproxima el voxel por superficies planas cuadradas (Figura 4-6). Este método genera gran cantidad de superficies (1 por voxel, como mínimo) pero es simple de implementar, ya que todas las superficies son simples de obtener y calcular.

Debido al tipo de equipamiento utilizado, nuestra investigación se centró en los métodos de surface rendering.
Dentro de esta línea, definimos dos tipos principales de estructuras de datos:
Esta estructura de datos representa los bordes del objeto en los distintos cortes (Figura 4-7). Teniendo esta información para cada slice podemos luego utilizarla como guía para derivar otras representaciones mas "complejas" o "completas" del objeto.

Una de las aplicaciones mas interesantes de esta estructura de datos es usarla como guía para aproximar la superficie del objeto mediante superficies bicúbicas spline [FOL91] [BAR82]. Este tipo de superficies matemáticas necesitan un conjunto de puntos entre los cuales interpolar. Generan una superficie c1 contínua y, por lo tanto, vistas muy atractivas del objeto. Además, ya que las superficies interpolan suavemente por si mismas entre los distintos cortes, se podría obviar el paso de interpolación de intensidades antes descripto.
Podría argumentarse que la interpolación es necesaria, igualmente, para tener mayor "densidad" de puntos guía sobre los cuales basar las curvas, pero basados en trabajos anteriores [BAR82], una mayor densidad en zonas de baja curvatura no mejora la imágen y sí aumenta la carga computacional.
Existen muchos paquetes comerciales de software que hacen el mapping de superficies suaves sobre un conjunto cerrado de puntos. En la (Figura 4-7) podemos observar la disposición espacial de los contornos nivelados. En la (Figura 4-8) vemos la representación producida por nuestro sistema de una vertebra por medio de contornos nivelados.

La construcción de la representación por contornos dirigidos nivelados tiene los siguientes pasos:

La representación por parches triangulares es útil debido a la rapidez con la que puede ser mostrada en pantalla. Si bién la resolución obtenida no es igual a la de superficies B-Spline, permite un manejo interactivo del órgano, ya que el tiempo de respuesta del rendering de un modelo wireframe basado en parches triangulares está muy optimizado y ha sido estudiado largamente en el área de Computer Graphics.
En la (Figura 4-11) se puede observar la superficie externa del cráneo representada mediante parches triangulares, según lo produce nuestro sistema.

Para obtener esta representación, se parte de la estructura de contornos dirigidos nivelados recién explicada. El algoritmo de triangulación es una adaptación del presentado en [EKO91], que a su vez es una extensión de [CHR788], [BOI85-1] y [BOI85-2]. En líneas generales, tiene los siguientes pasos:
Se tiene un número n de contornos en el nivel k (corte k) y un número s de contornos en el nivel k+1 (corte k+1).
La primer tarea es decidir que contorno(s) del nivel k se debe encadenar con que contorno(s) del nivel k+1. Se adopta la siguiente regla heurística: se calculan las áreas de solapamiento (overlapping) (Figura 4-12) entre cada uno de los contornos del nivel k con cada uno de los contornos del nivel k+1.

Este solapamiento se traduce en un porcentaje que se compara con un "umbral de certeza" (de 0 a 1) provisto por el usuario. Mientras mayor es el umbral de certeza mayor exactitud se pretende en las conexiones, pero mayor es también el riesgo de obviar una conexión necesaria que no superó el umbral quizás por errores en la adquisición de datos o en la registración de los distintos cortes. Es decir, se debe tomar una desición de compromiso balanceando la calidad que se pretende en la desición, con la calidad del equipamiento de pre-procesamiento que se dispone.
Un punto importante es la densidad de cortes. Si no se toma la cantidad de cortes necesaria se puede incurrir en el error de conectar erróneamente los contornos, como se aprecia en la (Figura 4-13).

A medida que se va tomando la desición de cómo realizar el encadenamiento se va formando una matriz de conexiones. (Figura 4-14). Al terminar el proceso de desición, esta matriz tiene todas las conexiones que hay que hacer entre los dos cortes k y k+1.

Los tipos de conexiones posibles (mostrados en Figura 4-15) son:

El método de generación de triángulos en el caso de Multiple-Branching es una extensión del caso general de Single-Branching, que se esboza a continuación:
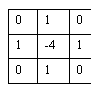
Dados C(k) y C(k+1), dos contornos dirigidos cerrados coplanares, en el corte k y k+1 respectivamente, generados uniformemente mediante una lista de vértices, la generación de parches triangulares que cubran (o interpolen) la superficie determinada por el promedio de la extrusión de ambos contornos a lo largo de un eje perpendicular al plano sobre el cual están inscriptos, se define como un secuencia de pasos, a saber:
Paso A: Siendo nv(k) y nv(k+1) el número de vértices de C(k) y C(k+1) respectivamente, se define (Figura 4-16):
nvMAX = max[nv(k), nv(k+1)]
nvMIN = min[nv(k), nv(k+1)]
Ca = C(k), Cb = C(k+1) si nvMAX = nv(k)
o también
Ca = C(k+1), Cb = C(k) si nvMAX = nv(k+1)
donde
Ca es el contorno con mayor número de vértices

Paso B: Para cada vértice de Cb se busca el vértice más "cercano" en Ca, manteniendo la localidad y sin generar cruzamientos. Se va generando un lista de bordes (BL) que representa las conexiones de cada vértice de Cb (campo vértice1) con alguno de Ca (campo vértice2).
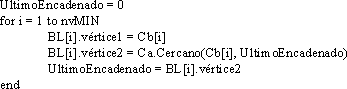
Luego de este paso, aplicado a la (Figura 4-16), tendriamos un situación como la mostrada en (Figura 4-17) y una tabla de bordes como (Figura 4-18).


Paso C: Se procesan, uno a uno, los vértices no encadenados de Ca, uniéndolos a los más próximos en Cb, de la siguiente manera:


En la segunda iteración, en cambio, v1=2 y v2=6, y (v2-v1) > 1, o sea, existen vértices entre v1 y v2 que no han sido conectados (Figura 4-20).

El loop sobre j procesa, uno por uno, los vértices de Ca que están entre v1 y v2. Para cada uno, se cálcula (función Distancia) la distancia a los vértices de Cb conectados a v1 y v2 respectivamente, eligiendose el mas cercano de estos para hacer la conexión. Se selecciona el mas cercano para no formar, en lo posible, triangulos largos y finos, que no se ven bien en el rendering. En la (Figura 4-21) tenemos la situación luego de la primer iteración en j.


Paso D: En este momento, tenemos la lista de bordes BL completa con todas las uniones que podemos hacer. Se ordena esta lista según el campo vértice2 (Figura 4-22) y se van procesando los bordes de a pares, generando los triángulos a partir de ellos siempre en sentido horario y siguiendo ciertas convenciones para permitir una mas fácil graficación, de la siguiente manera:

Si los bordes coinciden en algún vértice, se identifica este y se genera el único triángulo posible (Figura 4-24). En el ejemplo, los pares de bordes 2 y 3, 3 y 4, 4 y 5, y 5 y 6 serían ejemplos de este caso.


Para solucionar los problemas que presenta el método de Christiansen [CHR78} (Figura 4-25) al triangular dos contornos con siluetas disímiles, se transforman todos los contornos al máximo contorno convexo posible (convex-hull).

El convex-hull de un polígono es el máximo polígono convexo que lo contiene (Figura 4-26).

El algoritmo para obtener el convex hull de cualquier polígono es el siguiente:

En cada iteración, el algoritmo reduce (borra) todas las concavidades de primer orden, transformando por consiguiente las de 2do. en 1ero, etc. Eventualmente, no existirán mas concavidades y el polígono resultante es el convex-hull. La (Figura 4-27) ejemplifica la secuencia de iteraciones y sus resultados al aplicar el algoritmo al polígono de la (Figura 4-26).

La función Concavidad recibe tres puntos consecutivos y determina, basandose en una orientación definida como global para todo el sistema, si forman concavidad o nó.
Si es así, se elimina el vértice que genera la concavidad (el del medio) y se continúa procesando.
El procedimiento para encadenar dos contornos cualquiera, sería entonces:
La idea es usar los maximos contornos convexos para hacer el encadenamiento, ya que ambos, por la definición del algoritmo de desición para realizar encadenamiento (4.3.2.2.1), deberían tener formas similares. Obtenidas así las uniones (en términos de números de vértices y nó en coordenadas espaciales absolutas), se hace la analogía con los contornos originales y son estos, en definitiva, con los que se forman los triángulos.
Con este procedimiento, la (Figura 4-25) se transforma en (Figura 4-28).

Cuando un objeto tiene forma compleja, puede darse la situación mostrada en la (Figura 4-15b). En ese caso, es necesario encadenar un contorno de un nivel con varios de otro.
El procedimiento para lograr el encadenamiento se basa en lo visto anteriormente y consiste en la siguiente secuencia:
Dados Ck,1,Ck,2, ...,Ck,n; contornos en el nivel k; y Ck+1; contorno en el nivel k+1, el multiple branching entre los contornos de k, con los de k+1 se define como:
Como ejemplo, supongamos que tenemos tres contornos en un nivel k que debemos encadenar con un único contorno en un nivel k+1 (Figura 4-29).

Al unir los centroides de los tres contornos obtenemos el "contorno abarcador" mostrado en (Figura 4-30). Notesé que algunos vértices de los contornos que forman este "contorno abarcador" no forman parte de este último.

Realizamos el single branching entre el "contorno abarcador" y el contorno único del nivel k+1, pero nó generamos los triángulos respectivos, sinó que guardamos la tabla de bordes. En la (Figura 4-31) se observan los bordes generados luego de realizado este paso.

A un nivel intermedio entre los niveles k y k+1 formamos el contorno interpolado C'. Los vértices de este son, justamente, la intersección de c/u de los bordes generados en el paso anterior con un plano coplanar al plano que contiene los contornos en cuestión, pero al nivel Z = (Z(k) + Z(k+1)) / 2. (Figura 4-32).

Una vez generado el contorno C', hacemos el single branching entre este y el único contorno del nivel k+1. Esta vez, sin embargo, sí generamos los triángulos correspondientes. (Figura 4-33)

Debemos ahora, conectar cada contorno individual del nivel k con C'. Unimos entonces, los vértices de los contornos C(k,..) con sus proyecciones en C'. Pero con aquellos vértices que no formaron C', debemos tener una consideración especial.
Unimos cada uno de estos vértices con el vértice proyectado (sobre C') mas próximo. Si estamos sobre el último de estos vértices, debemos conectarlo a ambos extremos "proyectados" en C' (ver Figura 4-34).

Finalmente, debemos triangular en el plano de C', la zona que queda abierta para poder, así, cerrar el volumen. La zona a cerrar es la resta booleana de C' menos todos los contornos del nivel k. En la (Figura 4-35) se observa esta en línea de puntos.
El resultado de todo el proceso, a manera de un simple esquema, se muestra en la (Figura 4-36).

